上一篇分析完all-gather 用在communication的機制上後

這篇要接著來分析把任務散播出去(Scatter)

這張圖是說把手邊的東西，一個一個分別送出去

換成文言文來講就是把切好分好的那些Task們，分給處理器去計算！

但是一個一個分別散播出去的方法效能不佳

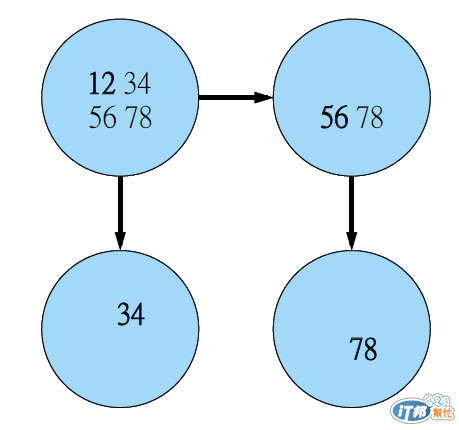
這個方法就比較有效率，時間複雜度為 Log (p)

如圖，每一回合都把手邊有的東西分一半出去

第一回合：一開始有 12345678 把 5678分出去

第二回合：現在一個點有 1234 另一個點有 5678，這次還是一樣，每個人都把手邊有的一半分出去，不要分到剛剛給你那個點

1234那個點把 34分出去， 5678那個點把 78 分出去

即完成！ 現在每個人都有任務，而且任務數量都是兩個：12, 34, 56, 78

分析：

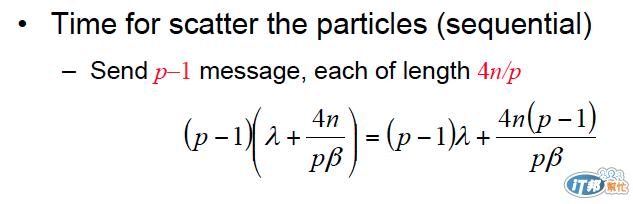
如果採用第一種方法的話 sequential 地下去分配，

如此 p 個點共要分 p-1 次，每次都會要加上延遲時間 lamda，每次分配的流量是 4n/pB 這裡的 beta 是頻寬寬度！

整理完的公式如圖所示

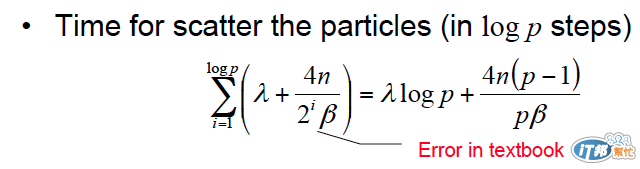
如果採用第二種方法只需要 log (p) 個步驟就可以做完，每次所需要分送的量以2^i 呈指數成長，所以i 從 1 加到 p 個回合就可以做完！

整理完後的公式如圖，發現跟第一種方法後面一項是一樣的，只差在前面那一項決定這兩種方法的快慢！

所以結論是：因為 入log p 在p數量大的情形下會比 (p-1)入 還要快，所以第二種方法比較快！